Vamos a analizar la siguiente relacion de dispersion
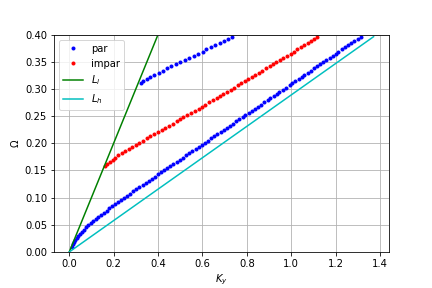
que se analiza en la siguiente liga: http://manza.space/2022-2/guia-discontinua/relacion-de-dispersion/
Vamos a analizar el caso para una frecuencia 0.1
import math
import numpy as np
import matplotlib.pyplot as plt
c = 3e8
d = 0.5e-6
nl = 1.0
nh = 3.6
el = nl*nl
eh = nh*nh
Om = 0.1
w = ((2.0*math.pi*c)/d)*Om
kl = nl*(w/c)
kh = nh*(w/c)
Nky = 100
kyi = nl*(w/c)
kyf = nh*(w/c)
dky = (kyf-kyi)/(Nky)
kyV = np.zeros(Nky)
aux1 = np.zeros(Nky)
aux2 = np.zeros(Nky)
qlxV = np.zeros(Nky)
khxV = np.zeros(Nky)
for iky in range(2,Nky-2):
ky = kyi+iky*dky
kyV[iky] = ky*(d/(2.0*math.pi))
qlx = math.sqrt(ky*ky-kl*kl)
khx = math.sqrt(kh*kh-ky*ky)
qlxV[iky] = qlx
khxV[iky] = khx
aux1[iky] = abs(qlx-khx*math.tan(0.5*khx*d))
aux2[iky] = abs(qlx+khx*(1.0/math.tan(0.5*khx*d)))
for iky in range(2,Nky-2):
if aux1[iky]<aux1[iky-1] and aux1[iky]<aux1[iky+1]:
print("par",iky,kyV[iky],"qlx=",qlxV[iky],",khx=",khxV[iky])
if aux2[iky]<aux2[iky-1] and aux2[iky]<aux2[iky+1]:
print("impar",iky,kyV[iky],"qlx=",qlxV[iky],",khx=",khxV[iky])
el resultado es
par 62 0.2612 qlx= 3032258.7195141893 ,khx= 3113178.7677315874
plt.plot(kyV,aux1,'b.')
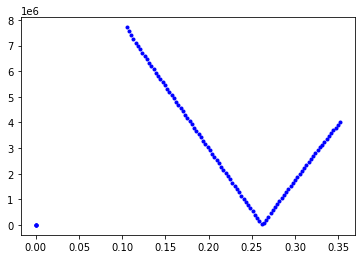
Om=0.2
impar 28 0.34559999999999996 qlx= 3541830.1643658113 ,khx= 7937338.2827297235 par 84 0.6367999999999999 qlx= 7597347.907542297 ,khx= 4222109.034530145
Om=0.35
par 24 0.5683999999999998 qlx= 5627974.468371605 ,khx= 14131002.155258968 impar 70 0.9869999999999999 qlx= 11596990.03063907 ,khx= 9842212.18821431 par 93 1.1962999999999997 qlx= 14375366.055158557 ,khx= 4970731.264992242