El siguiente programa nos permite visualizar los modos guiados. Para eso es necesario dar exactamente el vector de onda y frecuencia, los cuales se pueden obtener del post anterior.
Separamos en un programa par y otro programa impar.
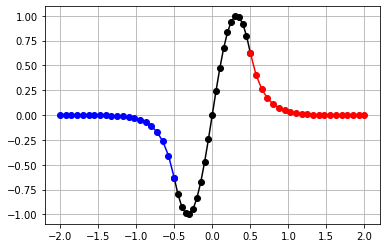
Modos par
qlx=13033816.300340246 khx=4849447.026609609 xi = -d/2 xf = d/2 Nx = 20 dx = (xf-xi)/Nx xVc = np.zeros(Nx+1) aux5 = np.zeros(Nx+1) aux6 = np.zeros(Nx+1) for ix in range(0,Nx+1): x = xi+ix*dx xVc[ix] = x/d aux5[ix] = math.cos(khx*x) A=math.cos(khx*0.5*d)/math.exp(-qlx*0.5*d) D=math.cos(khx*0.5*d)/math.exp(-qlx*0.5*d) xi = -2*d xf = -d/2 Nx = 20 dx = (xf-xi)/Nx xVl = np.zeros(Nx+1) aux7 = np.zeros(Nx+1) aux8 = np.zeros(Nx+1) for ix in range(0,Nx+1): x = xi+ix*dx xVl[ix] = x/d aux7[ix] = A*math.exp(qlx*x) xi = d/2 xf = 2*d Nx = 20 dx = (xf-xi)/Nx xVr = np.zeros(Nx+1) aux9 = np.zeros(Nx+1) aux10 = np.zeros(Nx+1) for ix in range(0,Nx+1): x = xi+ix*dx xVr[ix] = x/d aux9[ix] = D*math.exp(-qlx*x) plt.plot(xVc,aux5,'ko-') plt.plot(xVl,aux7,'bo-') plt.plot(xVr,aux9,'ro-') plt.grid() plt.show()
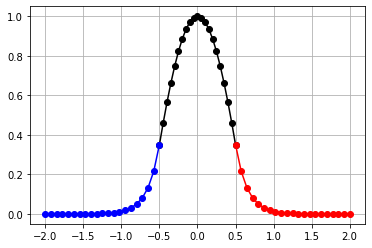
Podemos ver el segundo modo par si ponemos
qlx=5627974.468371605 khx=14131002.155258968
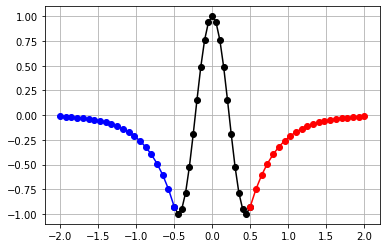
Modo impar
qlx=11596990.03063907 khx=9842212.18821431 xi = -d/2 xf = d/2 Nx = 20 dx = (xf-xi)/Nx xVc = np.zeros(Nx+1) aux5 = np.zeros(Nx+1) aux6 = np.zeros(Nx+1) for ix in range(0,Nx+1): x = xi+ix*dx xVc[ix] = x/d aux5[ix] = math.sin(khx*x) A=math.sin(-khx*0.5*d)/math.exp(-qlx*0.5*d) D=math.sin(khx*0.5*d)/math.exp(-qlx*0.5*d) xi = -2*d xf = -d/2 Nx = 20 dx = (xf-xi)/Nx xVl = np.zeros(Nx+1) aux7 = np.zeros(Nx+1) aux8 = np.zeros(Nx+1) for ix in range(0,Nx+1): x = xi+ix*dx xVl[ix] = x/d aux7[ix] = A*math.exp(qlx*x) xi = d/2 xf = 2*d Nx = 20 dx = (xf-xi)/Nx xVr = np.zeros(Nx+1) aux9 = np.zeros(Nx+1) aux10 = np.zeros(Nx+1) for ix in range(0,Nx+1): x = xi+ix*dx xVr[ix] = x/d aux9[ix] = D*math.exp(-qlx*x) plt.plot(xVc,aux5,'ko-') plt.plot(xVl,aux7,'bo-') plt.plot(xVr,aux9,'ro-') plt.grid() plt.show()