En el paper de los japoneses, se considera una guia con nh=3.6, nl=1.0 y una d=0.5e-6 m
import math
import numpy as np
c = 3e8
d = 0.5e-6
nl = 1.0
nh = 3.46
Omi = 0.01
Omf = 0.4
NOm = 100
dOm = (Omf-Omi)/NOm
Nky = 200
kyV = np.zeros(Nky)
f1 = np.zeros(Nky)
f2 = np.zeros(Nky)
f3 = np.zeros(Nky)
f4 = np.zeros(Nky)
f5 = np.zeros(Nky)
data1= open("data1.dat","w")
data2= open("data2.dat","w")
for iOm in range(0,NOm):
Om = Omi+iOm*dOm
w = ((2.0*math.pi*c)/d)*Om
kh = nh*(w/c)
kl = nl*(w/c)
# print(Om,w)
kyi = nl*(w/c)
kyf = nh*(w/c)
dky = (kyf-kyi)/(Nky-1)
for iky in range(1,Nky-1):
ky = kyi+iky*dky
qlx = math.sqrt(ky*ky-kl*kl)
khx = math.sqrt(kh*kh-ky*ky)
kyV[iky-1] = ky*(d/(2.0*math.pi))
f1[iky-1] = qlx
f2[iky-1] = khx*math.tan(0.5*khx*d)
f3[iky-1] = abs(f1[iky-1]-f2[iky-1])
f4[iky-1] = khx*(1.0/math.tan(0.5*khx*d))
f5[iky-1] = abs(f1[iky-1]+f4[iky-1])
for iky in range(1,Nky-1):
if f3[iky] < f3[iky-1] and f3[iky]<f3[iky+1]:
data1.write(str(kyV[iky])+" "+str(Om) + "\n")
if f5[iky] < f5[iky-1] and f5[iky]<f5[iky+1]:
data2.write(str(kyV[iky])+" "+str(Om) + "\n")
data1.close()
data2.close()
data3= open("data3.dat","w")
data3.write(str(0) +" "+str(0) +" "+str(0) + "\n")
data3.write(str(nl*Om) +" "+str(nh*Om) +" "+str(Om) + "\n")
data3.close()
Se grafica con
import matplotlib.pyplot as plt
data1 = np.loadtxt('data1.dat')
data2 = np.loadtxt('data2.dat')
data3 = np.loadtxt('data3.dat')
ky_par = data1[:, 0]
w_par = data1[:, 1]
ky_impar = data2[:, 0]
w_impar = data2[:, 1]
Ll = data3[:, 0]
Lh = data3[:, 1]
w = data3[:, 2]
#plt.figure(figsize=(3, 5))
#plt.figure(figsize=(cm_to_inch(5.),cm_to_inch(10)))
plt.plot(ky_par, w_par, 'b.',label="par" )
plt.plot(ky_impar, w_impar, 'r.',label="impar" )
plt.plot(Ll,w,'g-',label=r'$L_l$')
plt.plot(Lh,w,'c-',label=r'$L_h$')
plt.grid()
plt.legend(loc="upper left")
plt.ylim([0, 0.4])
#plt.ylim([0, 30])
plt.ylabel(r'$\Omega$')
plt.xlabel(r'$K_y$')
plt.savefig('plot.png')
plt.show()
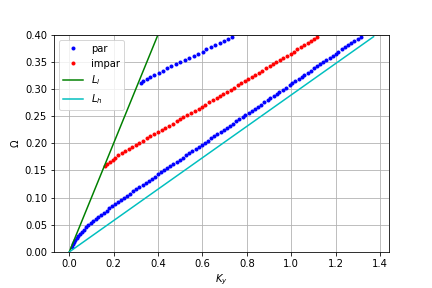
En la publicacion, se plantea que se excita el modo con una longitud de onda de lambda=1.55 e-6. Entonces tenemos que d/lambda=0.32. Observamos que a es frecuencia existen tres modos:
TE0 que es el primer modo par
TE1 que es el primer modo impar
TE2 que es el segundo modo par