integra

 

 

 

 

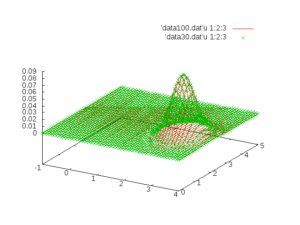
Y usando el programa

 

dd

 

Este programa fue el original con el que realizamos el articulo.

Sin embargo, para simular mediante el FDTD, necesitamos definir los intervalos espaciales y temporales de foma diferente.

Los intervalos espaciales se asignan de la siguiente manera:

 

 

 

Planteamos ahora esta version

 

[code language=”cpp”]

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
#include <complex>
#include <time.h>
using namespace std;
double pi = 2.0*asin(1.0);
double c = 343.0;

int main()
{
double f0=1000,t0=1.0/f0,x0=c*t0,w0=(2.0*pi)/t0,h,k0=w0/c,th=0.4*t0;
double s1,x1,k1,w1,f1;
int ix,Nx = 20;double x,dx=x0/double(Nx);
int it, Nt =400;double t,dt=x0/(2.0*Nx*c);
int itau,Ntau=50;double tau,taui=-1.0*t0,tauf=+4.0*t0,dtau=(tauf-taui)/float(Ntau);
int iw, Nw =50;double w, wi =+0.0*w0,wf =+5.0*w0,dw =(wf-wi) /float(Nw);
double xd,aux1,aux2,aux3,aux4,aux5;
double beta2_1,gamma_1,delta_1,FF1r,FF1i,FF1;

s1 = 0.3*x0;
x1 = 0.0*x0;
w1 = 2.0*w0;
k1 = w1/c;

cout << "frecuencia f0 = "<< f0 << " " << "\n";
cout << "tiempo referencia t0=1/f0 = "<< t0 << " " << "\n";
cout << "distancia de referencia x0=c*t0 = " << x0 << "\n";
cout << "dx =" << "\n";
cout << "dt =" << dt << "\n";
cout << "dt del fdtd " << x0/(20.0*2.0*c) << "\n";
cout << "\n";
cout << "Datos del pulso " << "\n";
cout << "s1 " << s1 << "\n";
cout << "x1 " << x1 << "\n";
cout << "f1 " << w1/(2.0*pi) << "\n";
cout << "k1 " << k1 << "\n";

xd = 3.0*x0;

ofstream myfile00;myfile00.open ("data00.dat");
for(it=0;it<=Nt;it++)
{
t = -(double(Nt)/2.0)*dt+float(it)*dt;
aux1 = exp( -(1.0/(2.0*s1*s1))*((xd-x1)-c*t)*((xd-x1)-c*t) );
aux2 = cos(k1*(xd-x1)-w1*t);
f1 = aux1*aux2;
myfile00 << t*1000.0 << " " << f1 << "\n";
}
myfile00.close();

ofstream myfile100;myfile100.open ("data100.dat");

for(itau=0;itau<=Ntau;itau++)
{
tau = taui+float(itau)*dtau;
beta2_1 = (c*c)/(s1*s1)+1.0/(th*th);
gamma_1 = ((xd-x1)*c)/(s1*s1)+tau/(th*th);
delta_1 = ((xd-x1)*(xd-x1))/(s1*s1)+(tau*tau)/(th*th);

for(iw=0;iw<=Nw;iw++)
{
w = wi+float(iw)*dw;

aux1 = exp( -0.5*delta_1+0.5*(gamma_1*gamma_1)/beta2_1 );
aux2 = exp( -0.5*((w-w1)*(w-w1))/beta2_1 );
aux3 = exp( -0.5*((w+w1)*(w+w1))/beta2_1 );
aux4 = +k1*(xd-x1)+(gamma_1/beta2_1)*(w-w1);
aux5 = -k1*(xd-x1)+(gamma_1/beta2_1)*(w+w1);
FF1r = (0.5/(sqrt(beta2_1)*th))*(aux1*(aux2*cos(aux4)+aux3*cos(aux5)));
FF1i = (0.5/(sqrt(beta2_1)*th))*(aux1*(aux2*sin(aux4)+aux3*sin(aux5)));
FF1 = FF1r*FF1r+FF1i*FF1i;

myfile100 << tau*1000.0 << " " << (w/(2.0*pi))*(1.0/1000.0) << " " << FF1 << "\n";
}
}
myfile100.close();

ofstream myfile30;myfile30.open ("data30.dat");
for(itau=0;itau<=Ntau;itau++)
{
tau = taui+float(itau)*dtau;
for(iw=0;iw<=Nw;iw++)
{
w = wi+float(iw)*dw;

FF1r = 0.0;
FF1i = 0.0;
for(it=0;it<=Nt;it++)
{
t = -(double(Nt)/2.0)*dt+float(it)*dt;
aux1 = exp( -(1.0/(2.0*s1*s1))*((xd-x1)-c*t)*((xd-x1)-c*t) );
aux2 = cos(k1*(xd-x1)-w1*t);
h = (1.0/(th*sqrt(2.0*pi)))*exp( -(0.5/(th*th))*(t-tau)*(t-tau) );
FF1r = FF1r + h*aux1*aux2*cos(w*t);
FF1i = FF1i + h*aux1*aux2*sin(w*t);
}
FF1r = dt*FF1r;
FF1i = dt*FF1i;
FF1 = FF1r*FF1r+FF1i*FF1i;
myfile30 << tau*1000.0 << " " << (w/(2.0*pi))*(1.0/1000.0) << " " << FF1 << "\n";
}
}
myfile30.close();

}

[/code]

 

en donde sale el mismo pulso en el dominio del tiempo

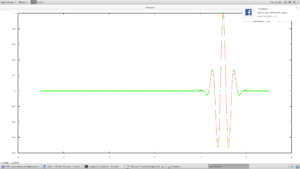
dd