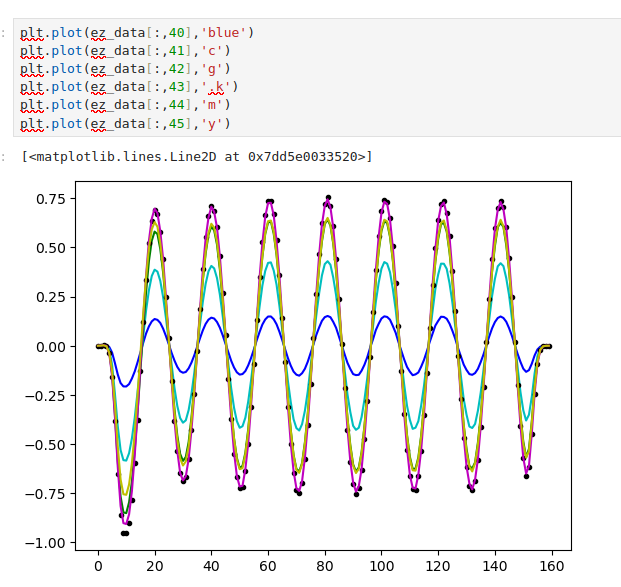
# From the Meep tutorial: plotting permittivity and fields of a straight waveguide
import meep as mp
cell = mp.Vector3(16, 8, 0)
geometry = [
mp.Block(
mp.Vector3(mp.inf, 1, mp.inf),
center=mp.Vector3(),
material=mp.Medium(epsilon=12),
)
]
sources = [
mp.Source(
mp.ContinuousSource(frequency=0.15), component=mp.Ez, center=mp.Vector3(-7, 0)
)
]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(
cell_size=cell,
boundary_layers=pml_layers,
geometry=geometry,
sources=sources,
resolution=resolution,
)
sim.run(until=200)
Ahi el programa corre, para visualizar tenemos
import matplotlib.pyplot as plt
import numpy as np
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.axis("off")
plt.show()
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.imshow(ez_data.transpose(), interpolation="spline36", cmap="RdBu", alpha=0.9)
plt.axis("off")
plt.show()

Es muy interesante darse cuenta de que ya tenemos los datos de la funcion dielectrica en python y los podemos visualizar haciendo
plt.imshow(eps_data)
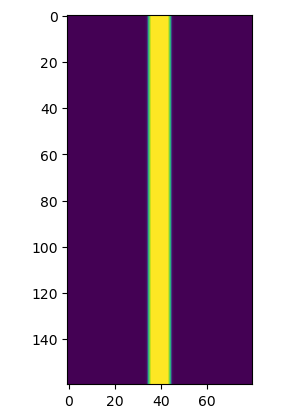
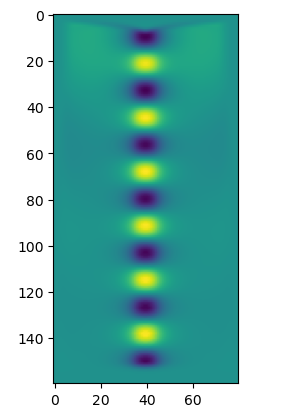
plt.imshow(ez_data)
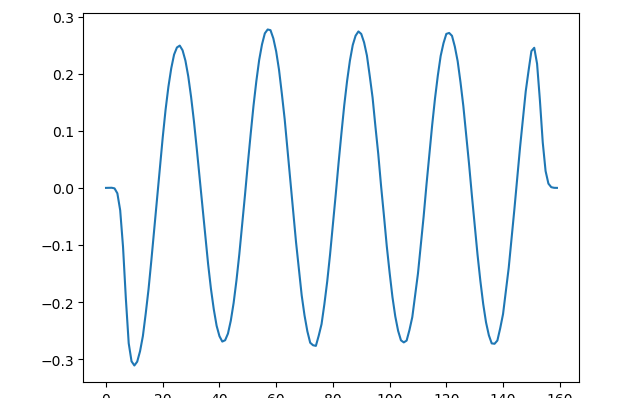
plt.plot(ez_data[:,40])
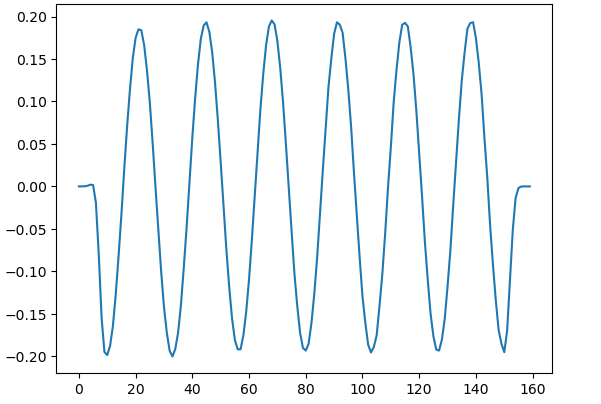
Vamos a entender la relacion de dispersion
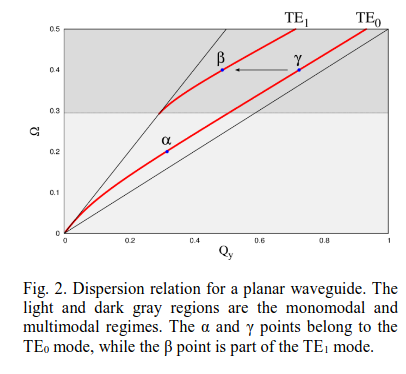
Esta es una guia de ![]() en aire (
en aire (![]() ).
).
import meep as mp cell = mp.Vector3(16, 8, 0) geometry = [mp.Block(mp.Vector3(mp.inf, 1, mp.inf),center=mp.Vector3(),material=mp.Medium(epsilon=4),)] sources = [mp.Source(mp.ContinuousSource(frequency=0.2), component=mp.Ez, center=mp.Vector3(-7, 0))] pml_layers = [mp.PML(1.0)] resolution = 10 sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,) sim.run(until=200)
import matplotlib.pyplot as plt
import numpy as np
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.axis("off")
plt.show()
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.imshow(ez_data.transpose(), interpolation="spline36", cmap="RdBu", alpha=0.9)
plt.axis("off")
plt.show()
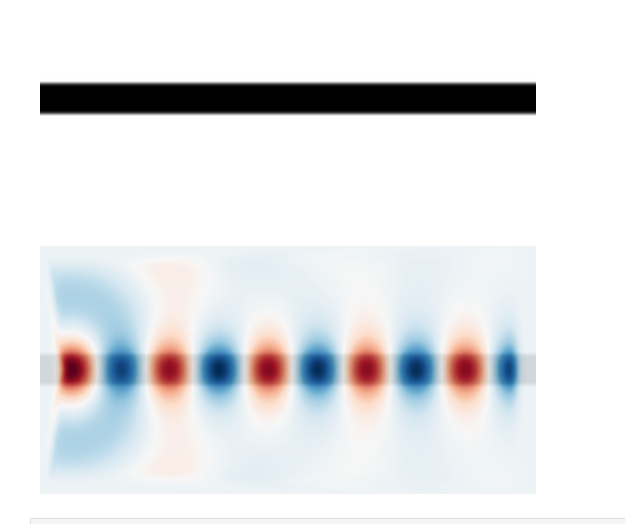
plt.plot(ez_data[:,40])
Para el modo en ![]() tenemos que
tenemos que ![]() , considerando que
, considerando que
![]()
![]()
![]()
Para el caso de ![]() tenemos
tenemos ![]()
Para poder medir la distancia entre valle y valle (o cresta y cresta), hacemos
f = open("python.dat","w")
for i in range(ez_data.shape[0]):
print(i,ez_data[i,40])
f.write(str(i/10.0)+" "+str(ez_data[i,40])+"\n")
f.close()
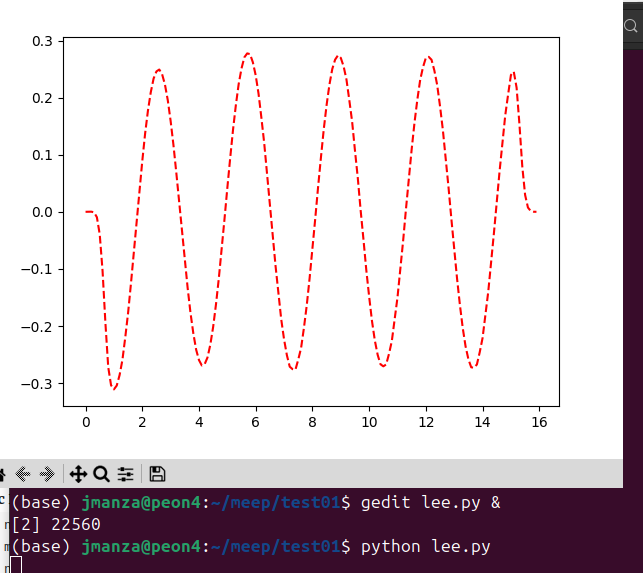
El siguiente codigo se llama lee.py y se corre en el sistema operativo para que se genere una grafica en donde con el mouse, se pueda medir las distancias
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt('python.dat')
x = data[:, 0]
y = data[:, 1]
plt.plot(x, y,'r--')
plt.show()
Cuando ![]() , tenemos
, tenemos ![]() , nos sale
, nos sale ![]() la longitud de onda, que e slo que vemos
la longitud de onda, que e slo que vemos
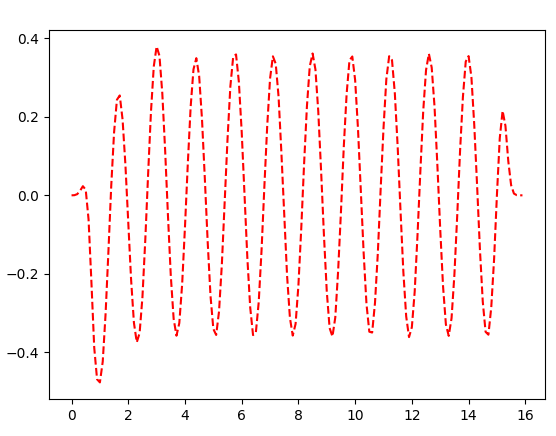
Podemos generar el segundo modo
# From the Meep tutorial: plotting permittivity and fields of a straight waveguide
import meep as mp
cell = mp.Vector3(16, 8, 0)
geometry = [mp.Block(mp.Vector3(mp.inf, 1, mp.inf),center=mp.Vector3(),material=mp.Medium(epsilon=4),)]
sources = [mp.Source(mp.ContinuousSource(frequency=0.4), component=mp.Ez, center=mp.Vector3(-7, 0.4),amplitude=+1.0),
mp.Source(mp.ContinuousSource(frequency=0.4), component=mp.Ez, center=mp.Vector3(-7, -0.4),amplitude=-1.0)]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,)
sim.run(until=200)
import matplotlib.pyplot as plt
import numpy as np
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.axis("off")
plt.show()
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.imshow(ez_data.transpose(), interpolation="spline36", cmap="RdBu", alpha=0.9)
plt.axis("off")
plt.show()
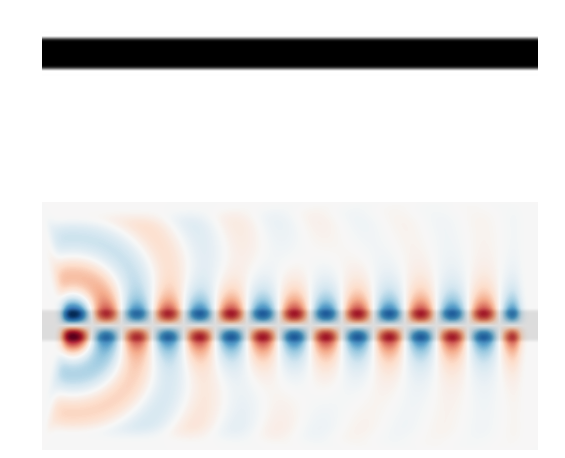
Podemos checar que la maxima amplitud NO esta en el centro