Primero entendemos como varian alfa y beta
for alfa in range(-2,3):
for beta in range(-2,3):
print(alfa,beta)
a_x=10
a_y=8.6
b_x=10
b_y=-8.6
for alfa in range(-2,3):
for beta in range(-2,3):
R_x=alfa*a_x+beta*b_x
R_y=alfa*a_y+beta*b_y
print(alfa,beta,R_x,R_y)
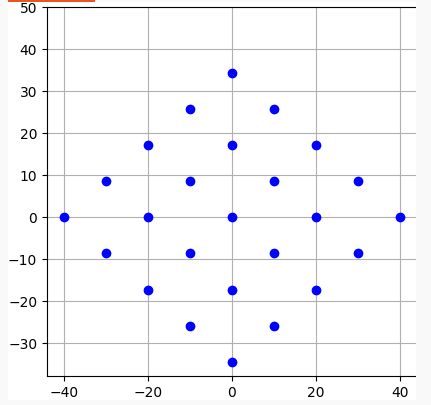
import matplotlib.pyplot as plt
a_x=10
a_y=8.6
b_x=10
b_y=-8.6
for alfa in range(-2,3):
for beta in range(-2,3):
R_x=alfa*a_x+beta*b_x
R_y=alfa*a_y+beta*b_y
print(alfa,beta,R_x,R_y)
plt.plot(R_x,R_y,'ob')
plt.grid()
plt.axis('square')
plt.show()
-2 -2 -40 0.0 -2 -1 -30 -8.6 -2 0 -20 -17.2 -2 1 -10 -25.799999999999997 -2 2 0 -34.4 -1 -2 -30 8.6 -1 -1 -20 0.0 -1 0 -10 -8.6 -1 1 0 -17.2 -1 2 10 -25.799999999999997 0 -2 -20 17.2 0 -1 -10 8.6 0 0 0 0.0 0 1 10 -8.6 0 2 20 -17.2 1 -2 -10 25.799999999999997 1 -1 0 17.2 1 0 10 8.6 1 1 20 0.0 1 2 30 -8.6 2 -2 0 34.4 2 -1 10 25.799999999999997 2 0 20 17.2 2 1 30 8.6 2 2 40 0.0
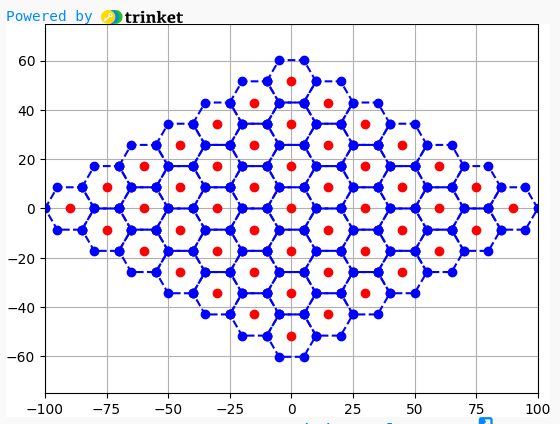
import matplotlib.pyplot as plt
import numpy as np
def ejes(max):
hx=np.array([-max,max])
hy=np.array([0,0])
plt.plot(hx,hy,'-k',linewidth=2)
vx=np.array([0,0])
vy=np.array([-max,max])
plt.plot(vx,vy,'-k',linewidth=2)
def hexagono(cx,cy):
x1 = np.array([cx])
y1 = np.array([cy])
#plt.plot(x1,y1,'ob')
x5=np.array([cx-10,cx-5 ,cx+5 ,cx+10,cx+5 ,cx-5 ,cx-10])
y5=np.array([cy+0 ,cy+8.6,cy+8.6,cy+0 ,cy-8.6,cy-8.6,cy+0])
plt.plot(x5,y5,'--ob')
a_x=15
a_y=8.6
b_x=15
b_y=-8.6
for alfa in range(-3,4):
for beta in range(-3,4):
R_x=alfa*a_x+beta*b_x
R_y=alfa*a_y+beta*b_y
hexagono(R_x,R_y)
plt.plot(R_x,R_y,'or')
plt.grid()
plt.axis('square')
plt.xlim(-100,100)
plt.ylim(-75,75)
plt.show()
https://trinket.io/embed/python3