Consideremos el analisis
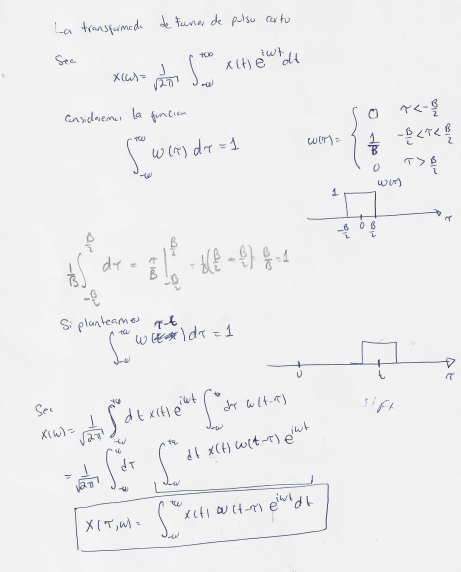
Una buena explicacion del metodo viene en
https://en.wikipedia.org/wiki/Short-time_Fourier_transform
import numpy as np
from scipy.io.wavfile import write
import math
import matplotlib.pyplot as plt
## PARAMETROS DE LA SENIAL
amplitud = 32767 # Amplitud máxima (para 16-bit PCM)
fs = 44100 # Frecuencia de muestreo en Hz (común para audio de alta calidad)
ts = 1/fs
## PARAMETROS DE LA SENIAL
f0 = 330
t0 = 1/f0
ti = 0.0
tf = 10*t0
Nt = int((tf-ti)*fs)
t = np.zeros(Nt+1)
st = np.zeros(Nt+1)
w = np.zeros(Nt+1)
tau = 0.7*tf
B = 3*t0
for it in range(Nt+1):
t[it] = ti+it*ts
st[it] = math.sin(2.0*math.pi*f0*t[it])
if t[it] > tau-0.5*B and t[it]<tau+0.5*B:w[it]=1.0
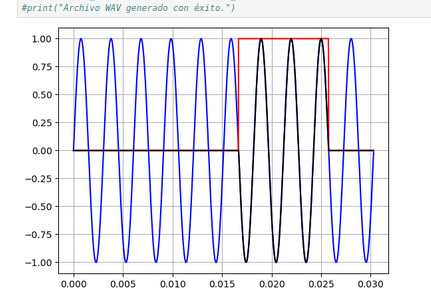
plt.plot(t,st,'b')
plt.plot(t,w,'r')
plt.plot(t,st*w,'k')
plt.grid()
plt.show()
senal = amplitud*st
senal_int16 = np.int16(senal)
write("senal_sinusoidal.wav", fs, senal_int16)
print("Archivo WAV generado con éxito.")
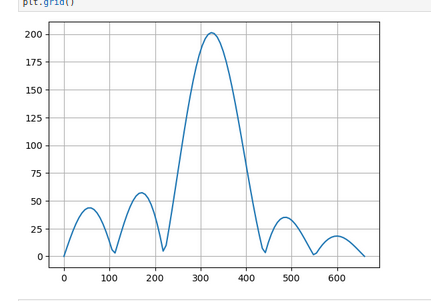
Nf = 100 f = np.zeros(Nf+1) sfr = np.zeros(Nf+1) sfi = np.zeros(Nf+1) sf = np.zeros(Nf+1) fi = 0.0 ff = 2.0*f0 df = (ff-fi)/Nf for iff in range(Nf+1): f[iff] = fi + iff*df for it in range(Nt+1): sfr[iff] = sfr[iff]+st[it]*w[it]*math.cos(2.0*math.pi*f[iff]*t[it]) sfi[iff] = sfi[iff]+st[it]*w[it]*math.sin(2.0*math.pi*f[iff]*t[it]) sf[iff] = math.sqrt( sfr[iff]**2 + sfi[iff]**2 ) plt.plot(f,sf) plt.grid()
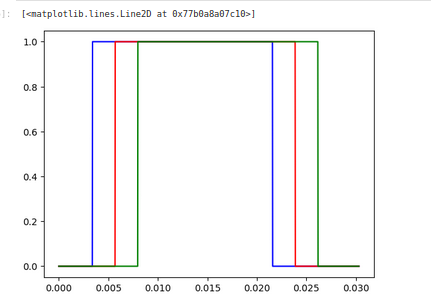
taui = 0.0*tf tauf = 1.0*tf Ntau = Nt dtau = (tauf-taui)/Ntau tauV = np.zeros(Ntau+1) w = np.zeros((Nt+1,Ntau+1)) B = 6*t0 for itau in range(Ntau+1): tauV[itau] = taui+itau*dtau for it in range(Nt+1): if t[it] > tauV[itau]-0.5*B and t[it]<tauV[itau]+0.5*B:w[it,itau]=1.0 plt.plot(t,w[:,550],'b') plt.plot(t,w[:,651],'r') plt.plot(t,w[:,752],'g')
stftr = np.zeros((Nf+1,Ntau+1)) stfti = np.zeros((Nf+1,Ntau+1)) stft = np.zeros((Nf+1,Ntau+1)) fi = 0.0 ff = 2.0*f0 df = (ff-fi)/Nf for itau in range(Ntau+1): for iff in range(Nf+1): f[iff] = fi + iff*df for it in range(Nt+1): stftr[iff,itau] = stftr[iff,itau]+st[it]*w[it,itau]*math.cos(2.0*math.pi*f[iff]*t[it]) stfti[iff,itau] = stfti[iff,itau]+st[it]*w[it,itau]*math.sin(2.0*math.pi*f[iff]*t[it]) stft[iff,itau] = math.sqrt( stftr[iff,itau]**2 + stfti[iff,itau]**2 )
plt.pcolormesh(tauV, f, np.abs(stft), shading='gouraud')
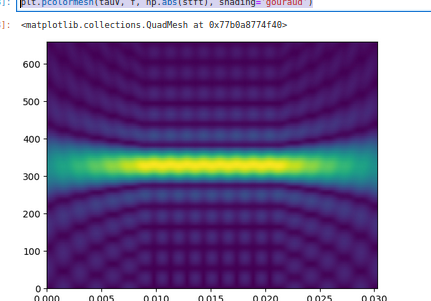
from matplotlib.gridspec import GridSpec
# Crear figura
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(2, 2, height_ratios=[1, 1], width_ratios=[1, 2]) # Ajusta la relación de anchos
# Subpanel superior derecho
ax1 = fig.add_subplot(gs[0, 1]) # 2 filas, 2 columnas, segundo panel
ax1.plot(t, st, 'b')
ax1.set_title("Señal en el Tiempo")
ax1.set_xlabel("Tiempo (s)")
ax1.set_ylabel("Amplitud")
# Subpanel inferior derecho
ax2 = fig.add_subplot(gs[1, 0]) # 2 filas, 2 columnas, tercer panel
ax2.plot( -1*sf,f, 'b')
ax2.set_title("Gráfica de -sw")
ax2.set_xlabel("Valor Negativo")
ax2.set_ylabel("Frecuencia")
# Subpanel inferior izquierdo con imshow
ax3 = fig.add_subplot(gs[1, 1]) # Ocupa toda la columna izquierda
#cax = ax3.imshow(stft, cmap='viridis', interpolation='nearest')
cax = ax3.pcolormesh(tauV, f, np.abs(stft), shading='gouraud')
ax3.set_title("STFT")
ax3.set_xlabel("tiempo")
ax3.set_ylabel("frecuencia")
# fig.colorbar(cax, ax=ax3) # Agregar barra de color si es necesario
plt.tight_layout()
plt.show()
