Autor: new.jmanza@gmail.com
Protegido: Guia recta, pocos pasos
Protegido: Investigacion con meep
doblez3 y la FT como funcion de H
import meep as mp
import numpy as np
import math
from matplotlib import pyplot as plt
############## -> H
NH = 220
Hi = 0.0
Hf = 11
dH = (Hf-Hi)/(NH)
HV = np.zeros(NH)
maxV = np.zeros(NH)
QQxV = np.zeros(NH)
maxV = np.zeros(NH)
############# <- H
############# -> FT
i_0=500
i_I=800
I=i_I-i_0
Qx_i=0.01
Qx_f=1.0
NQx=100
dQx=(Qx_f-Qx_i)/NQx
EQx=np.zeros(NQx)
QxV=np.zeros(NQx)
mapaFT=np.zeros((NH,NQx))
############ <- FT
for iH in range(NH):
H = Hi+iH*dH
HV[iH] = H
print(iH,H)
############################################### -> meep
L = 40
t_until=400
cell = mp.Vector3(2*L, L, 0)
geometry = [mp.Block(mp.Vector3(L, 1, mp.inf),center=mp.Vector3(-L/2,-H/2),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0]),
mp.Block(mp.Vector3(1,H+1, mp.inf),center=mp.Vector3( 0, 0),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0]),
mp.Block(mp.Vector3(L, 1, mp.inf),center=mp.Vector3(+L/2,+H/2),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0])]
sources = [mp.Source(mp.ContinuousSource(frequency=0.1), component=mp.Ez, center=mp.Vector3(-L+2, -H/2))]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,)
print('----------------- H = ',H)
plt.figure(dpi=100)
sim.plot2D()
plt.savefig('a'+str(H)+'.png')
plt.show()
sim.run(until=t_until)
plt.figure(dpi=100)
sim.plot2D(fields=mp.Ez)
plt.savefig('b'+str(H)+'.png')
plt.show()
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.imshow(eps_data)
plt.savefig('c'+str(H)+'.png')
plt.show()
plt.imshow(ez_data)
plt.savefig('d'+str(H)+'.png')
plt.show()
plt.plot(ez_data[:,int((L/2+H/2)*10)])
plt.savefig('e'+str(H)+'.png')
plt.show()
################################################## <- meep
################################################## -> FT
for iQx in range(NQx):
Qx = Qx_i+iQx*dQx
QxV[iQx]=Qx
Exr=0
Exi=0
for i in range(I):
Exr=Exr+ez_data[i_0+i,int((L/2+H/2)*10)]*math.cos(2.0*math.pi*Qx*((i_0+i)/resolution))
Exi=Exi+ez_data[i_0+i,int((L/2+H/2)*10)]*math.sin(2.0*math.pi*Qx*((i_0+i)/resolution))
EQx[iQx] = math.sqrt(Exr*Exr+Exi*Exi)
mapaFT[iH,iQx]=EQx[iQx]
plt.plot(QxV,EQx)
plt.savefig('f'+str(H)+'.png')
plt.show()
maxV[iH] = np.max(EQx)
el_indice = np.argmax(EQx)
QQxV[iH] = QxV[el_indice]
#################################################### <- FT
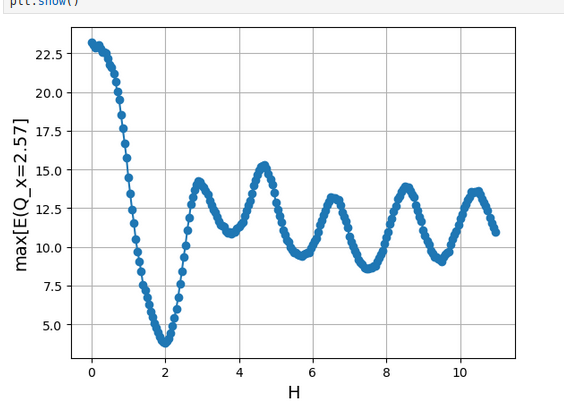
plt.plot(HV,maxV,'-o')
plt.xlabel('H', fontsize=14)
plt.ylabel('max[E(Q_x=2.57]', fontsize=14)
# Mostrar la gráfica
plt.grid()
plt.show()
Entendiendo las tripas del meep: doblez2 y la FT
import meep as mp
L = 40
H = 1
t_until=400
cell = mp.Vector3(2*L, L, 0)
geometry = [mp.Block(mp.Vector3(L, 1, mp.inf),center=mp.Vector3(-L/2,-H/2),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0]),
mp.Block(mp.Vector3(1,H+1, mp.inf),center=mp.Vector3( 0, 0),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0]),
mp.Block(mp.Vector3(L, 1, mp.inf),center=mp.Vector3(+L/2,+H/2),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0])]
sources = [mp.Source(mp.ContinuousSource(frequency=0.1), component=mp.Ez, center=mp.Vector3(-L+2, -H/2))]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,)
from matplotlib import pyplot as plt
plt.figure(dpi=100)
sim.plot2D()
plt.show()
sim.run(until=t_until)
plt.figure(dpi=100)
sim.plot2D(fields=mp.Ez)
plt.show()
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
print(ez_data.shape)
plt.imshow(ez_data)
plt.plot(ez_data[:,200],'-k') plt.plot(ez_data[:,210],'-b') plt.plot(ez_data[:,220],'-g') plt.plot(ez_data[:,230],'-r')
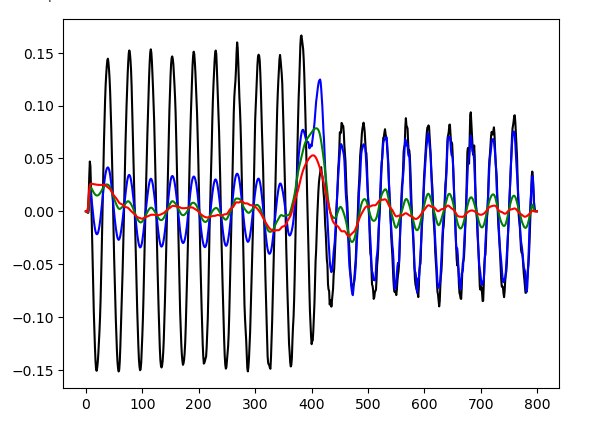
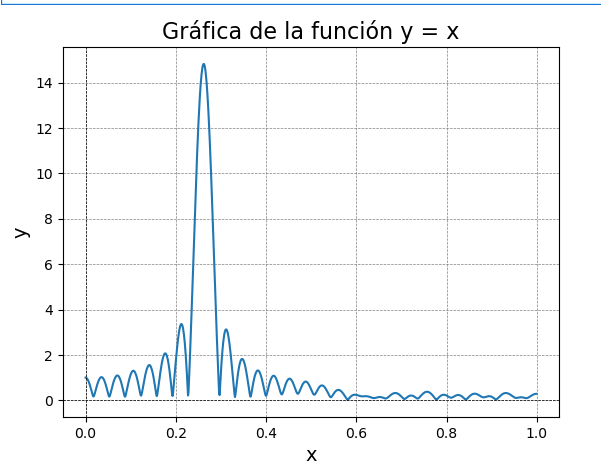
import numpy as np import math ############ FT i_0=500 i_I=800 I=i_I-i_0 Qx_i=0.0 Qx_f=1.0 NQx=1000 dQx=(Qx_f-Qx_i)/NQx EQx=np.zeros(NQx) QxV=np.zeros(NQx) ############# FT for ic in range(NQx): Qx = Qx_i+ic*dQx QxV[ic]=Qx Exr=0 Exi=0 for i in range(I): Exr=Exr+ez_data[i_0+i,int((L/2+H/2)*10)]*math.cos(2.0*math.pi*Qx*(i_0+i)/resolution) Exi=Exi+ez_data[i_0+i,int((L/2+H/2)*10)]*math.sin(2.0*math.pi*Qx*(i_0+i)/resolution) EQx[ic] = math.sqrt(Exr*Exr+Exi*Exi)
plt.plot(QxV,EQx)
# Graficar
# Personalización de la gráfica
plt.title('Gráfica de la función y = x', fontsize=16)
plt.xlabel('x', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.axhline(0, color='black',linewidth=0.5, ls='--') # Línea horizontal en y=0
plt.axvline(0, color='black',linewidth=0.5, ls='--') # Línea vertical en x=0
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
# Mostrar la gráfica
plt.show()
Entiendo las tripas del meep: doblez
import meep as mp
L = 40
H = 2
t_until=400
cell = mp.Vector3(2*L, L, 0)
geometry = [mp.Block(mp.Vector3(L, 1, mp.inf),center=mp.Vector3(-L/2,-H/2),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0]),
mp.Block(mp.Vector3(1,H+1, mp.inf),center=mp.Vector3( 0, 0),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0]),
mp.Block(mp.Vector3(L, 1, mp.inf),center=mp.Vector3(+L/2,+H/2),material=mp.Medium(epsilon=3.6*3.6),e1=[1.0, 0.0],e2=[0.0, 1.0])]
sources = [mp.Source(mp.ContinuousSource(frequency=0.1), component=mp.Ez, center=mp.Vector3(-L+2, -H/2))]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,)
from matplotlib import pyplot as plt
plt.figure(dpi=100)
sim.plot2D()
plt.savefig('books_read'+str(H)+'.png')
plt.show()
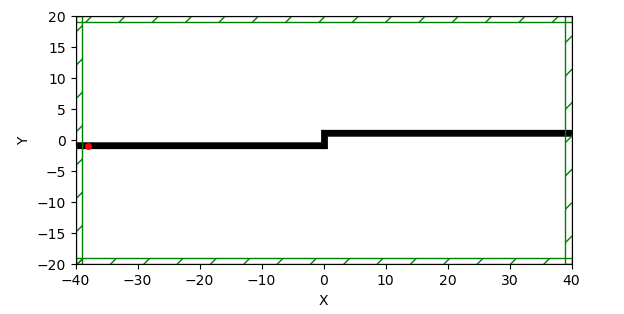
sim.run(until=t_until) plt.figure(dpi=100) sim.plot2D(fields=mp.Ez) plt.show()
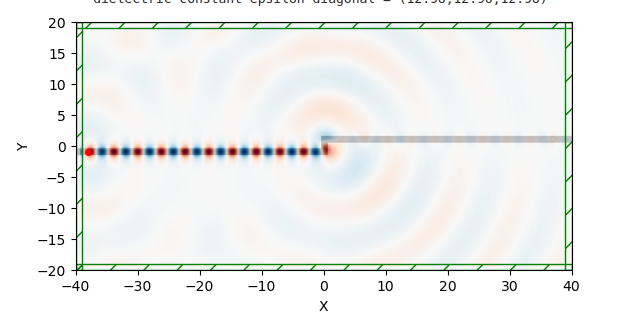
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data, interpolation='spline36', cmap='binary')
plt.imshow(ez_data, interpolation='spline36', cmap='RdBu', alpha=0.9)
plt.axis('off')
plt.show()
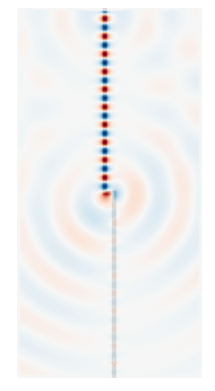
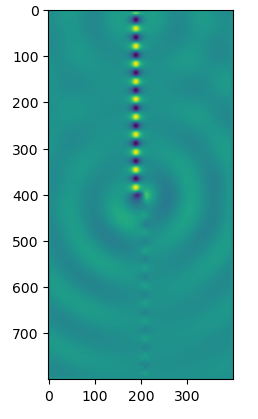
plt.imshow(ez_data)
plt.imshow(eps_data)
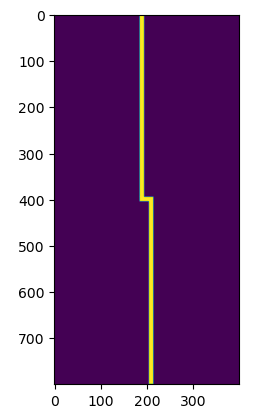
La guia recta
# From the Meep tutorial: plotting permittivity and fields of a straight waveguide
import meep as mp
cell = mp.Vector3(16, 8, 0)
geometry = [
mp.Block(
mp.Vector3(mp.inf, 1, mp.inf),
center=mp.Vector3(),
material=mp.Medium(epsilon=12),
)
]
sources = [
mp.Source(
mp.ContinuousSource(frequency=0.15), component=mp.Ez, center=mp.Vector3(-7, 0)
)
]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(
cell_size=cell,
boundary_layers=pml_layers,
geometry=geometry,
sources=sources,
resolution=resolution,
)
sim.run(until=200)
Ahi el programa corre, para visualizar tenemos
import matplotlib.pyplot as plt
import numpy as np
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.axis("off")
plt.show()
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.imshow(ez_data.transpose(), interpolation="spline36", cmap="RdBu", alpha=0.9)
plt.axis("off")
plt.show()

Es muy interesante darse cuenta de que ya tenemos los datos de la funcion dielectrica en python y los podemos visualizar haciendo
plt.imshow(eps_data)
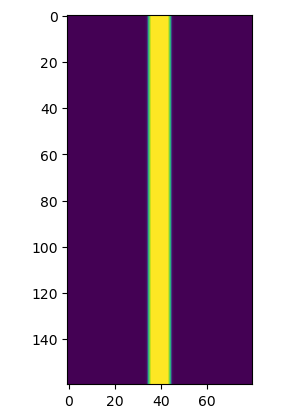
plt.imshow(ez_data)
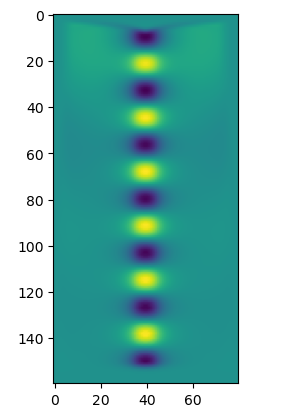
plt.plot(ez_data[:,40])
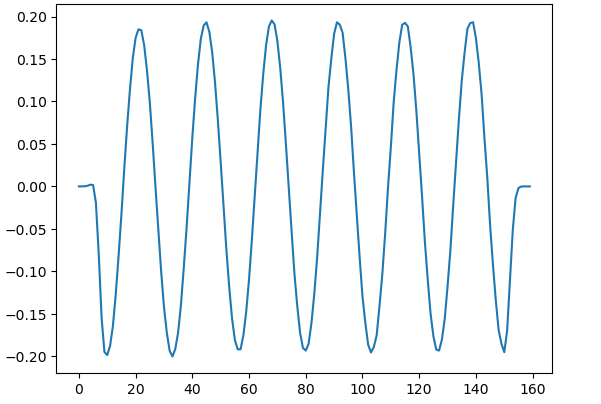
Vamos a entender la relacion de dispersion
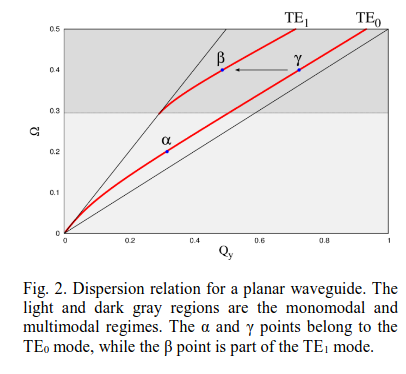
Esta es una guia de ![]() en aire (
en aire (![]() ).
).
import meep as mp cell = mp.Vector3(16, 8, 0) geometry = [mp.Block(mp.Vector3(mp.inf, 1, mp.inf),center=mp.Vector3(),material=mp.Medium(epsilon=4),)] sources = [mp.Source(mp.ContinuousSource(frequency=0.2), component=mp.Ez, center=mp.Vector3(-7, 0))] pml_layers = [mp.PML(1.0)] resolution = 10 sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,) sim.run(until=200)
import matplotlib.pyplot as plt
import numpy as np
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.axis("off")
plt.show()
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.imshow(ez_data.transpose(), interpolation="spline36", cmap="RdBu", alpha=0.9)
plt.axis("off")
plt.show()
plt.plot(ez_data[:,40])
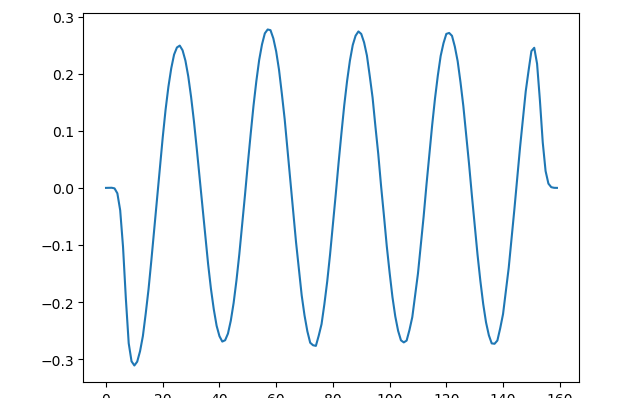
Para el modo en ![]() tenemos que
tenemos que ![]() , considerando que
, considerando que
![]()
![]()
![]()
Para el caso de ![]() tenemos
tenemos ![]()
Para poder medir la distancia entre valle y valle (o cresta y cresta), hacemos
f = open("python.dat","w")
for i in range(ez_data.shape[0]):
print(i,ez_data[i,40])
f.write(str(i/10.0)+" "+str(ez_data[i,40])+"\n")
f.close()
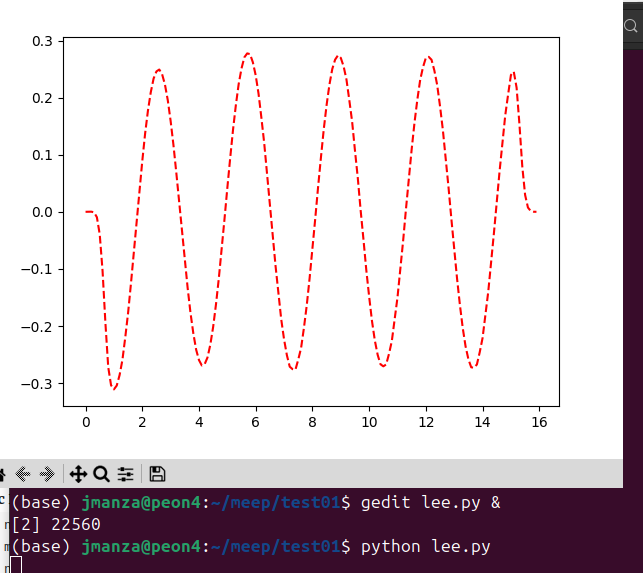
El siguiente codigo se llama lee.py y se corre en el sistema operativo para que se genere una grafica en donde con el mouse, se pueda medir las distancias
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt('python.dat')
x = data[:, 0]
y = data[:, 1]
plt.plot(x, y,'r--')
plt.show()
Cuando ![]() , tenemos
, tenemos ![]() , nos sale
, nos sale ![]() la longitud de onda, que e slo que vemos
la longitud de onda, que e slo que vemos
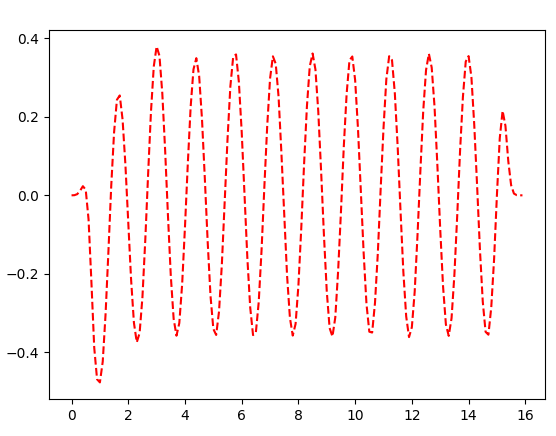
Podemos generar el segundo modo
# From the Meep tutorial: plotting permittivity and fields of a straight waveguide
import meep as mp
cell = mp.Vector3(16, 8, 0)
geometry = [mp.Block(mp.Vector3(mp.inf, 1, mp.inf),center=mp.Vector3(),material=mp.Medium(epsilon=4),)]
sources = [mp.Source(mp.ContinuousSource(frequency=0.4), component=mp.Ez, center=mp.Vector3(-7, 0.4),amplitude=+1.0),
mp.Source(mp.ContinuousSource(frequency=0.4), component=mp.Ez, center=mp.Vector3(-7, -0.4),amplitude=-1.0)]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,)
sim.run(until=200)
import matplotlib.pyplot as plt
import numpy as np
eps_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Dielectric)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.axis("off")
plt.show()
ez_data = sim.get_array(center=mp.Vector3(), size=cell, component=mp.Ez)
plt.figure()
plt.imshow(eps_data.transpose(), interpolation="spline36", cmap="binary")
plt.imshow(ez_data.transpose(), interpolation="spline36", cmap="RdBu", alpha=0.9)
plt.axis("off")
plt.show()
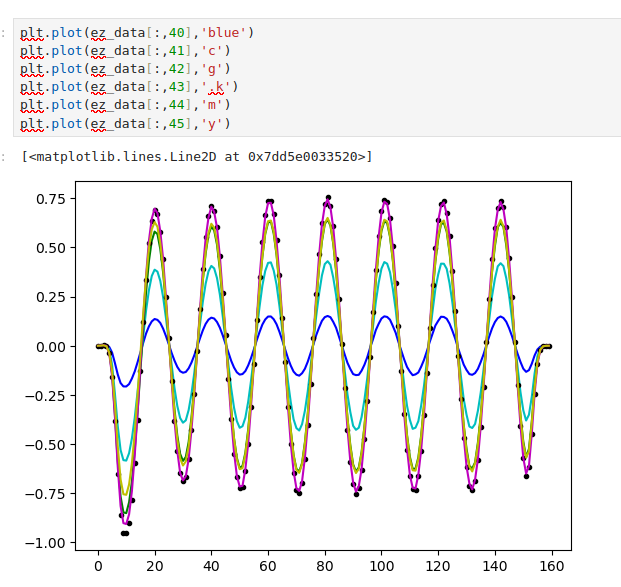
Podemos checar que la maxima amplitud NO esta en el centro
eje temporal
# From the Meep tutorial: plotting permittivity and fields of a straight waveguide
import meep as mp
cell = mp.Vector3(10, 10, 0)
geometry = [mp.Block(mp.Vector3(0.1, 0.1, mp.inf),center=mp.Vector3(4,4),material=mp.Medium(epsilon=1.1),)]
sources = [mp.Source(mp.ContinuousSource(frequency=0.8), component=mp.Ez, center=mp.Vector3(0, 0))]
pml_layers = [mp.PML(1.0)]
resolution = 10
sim = mp.Simulation(cell_size=cell,boundary_layers=pml_layers,geometry=geometry,sources=sources,resolution=resolution,)
sim.run(mp.at_beginning(mp.output_epsilon),mp.to_appended("ez", mp.at_every(0.05, mp.output_efield_z)),until=20)
Initializing structure...
time for choose_chunkdivision = 8.29697e-05 s
Working in 2D dimensions.
Computational cell is 10 x 10 x 0 with resolution 10
block, center = (4,4,0)
size (0.1,0.1,1e+20)
axes (1,0,0), (0,1,0), (0,0,1)
dielectric constant epsilon diagonal = (1.1,1.1,1.1)
time for set_epsilon = 0.019645 s
-----------
creating output file "./eps-000000.00.h5"...
creating output file "./ez.h5"...
run 0 finished at t = 20.0 (400 timesteps)
import h5py
import numpy as np
# Abre el archivo HDF5 en modo lectura
with h5py.File('eps-000000.00.h5', 'r') as f:
# Muestra las claves principales del archivo
print(f"Claves principales del archivo: {list(f.keys())}")
with h5py.File('eps-000000.00.h5', 'r') as f:
dataset = f['eps']
data_array = np.array(dataset)
import matplotlib.pyplot as plt plt.imshow(data_array)
import h5py
import numpy as np
# Abre el archivo HDF5 en modo lectura
with h5py.File('ez.h5', 'r') as f:
# Muestra las claves principales del archivo
print(f"Claves principales del archivo: {list(f.keys())}")
with h5py.File('ez.h5', 'r') as f:
dataset2 = f['ez']
data_array2 = np.array(dataset2)
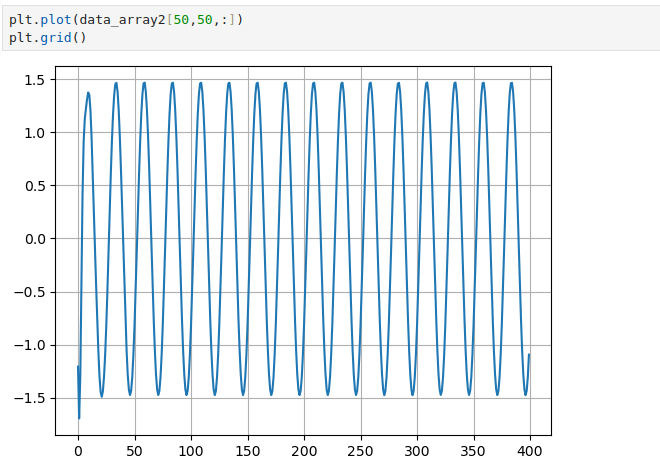
import math
shapes = data_array2.shape
d = 1e-6
c = 3e8
untill = 20
ti = 0
tf = untill
dt = (tf-ti)/shapes[2]
time = np.zeros(shapes[2])
signal = np.zeros(shapes[2])
auxi1 = np.zeros(shapes[2])
auxi2 = np.zeros(shapes[2])
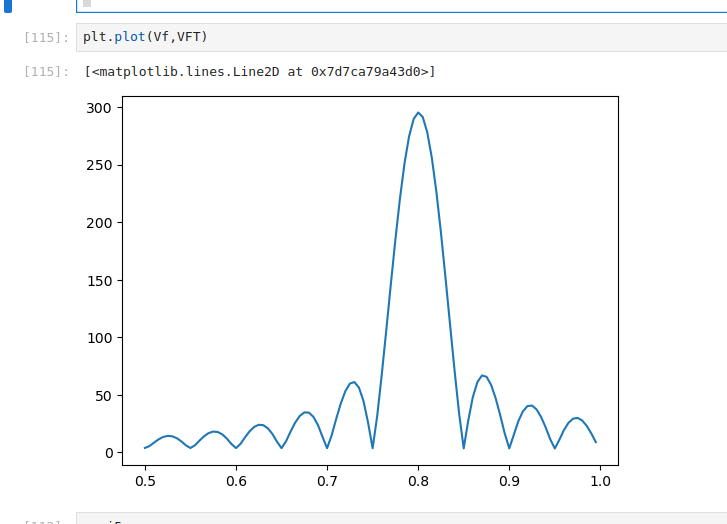
fi = 0.5
ff = 1.0
Nf = 100
df = (ff-fi)/Nf
Vf = np.zeros(Nf)
VFT = np.zeros(Nf)
for iff in range(Nf):
f = fi+iff*df
Vf[iff] = f
auxi3 = 0
auxi4 = 0
for i in range(shapes[2]):
time[i] = ti+i*dt
signal[i] = data_array2[50,50,i]
auxi1[i] = math.cos(2.0*math.pi*f*time[i])
auxi2[i] = math.sin(2.0*math.pi*f*time[i])
auxi3=auxi3+signal[i]*auxi1[i]
auxi4=auxi4+signal[i]*auxi2[i]
auxi5 = math.sqrt(auxi3*auxi3+auxi4*auxi4)
VFT[iff]=auxi5
los archivos h5
Esta es una leccion que aprendimos gracias a chatgpt. Dice que primero ha que instalar “pip install h5py numpy”
import h5py
import numpy as np
# Abre el archivo HDF5 en modo lectura
with h5py.File('eps-000000.00.h5', 'r') as f:
# Muestra las claves principales del archivo
print(f"Claves principales del archivo: {list(f.keys())}")
Claves principales del archivo: ['eps']
with h5py.File('eps-000000.00.h5', 'r') as f:
dataset = f['eps']
data_array = np.array(dataset)
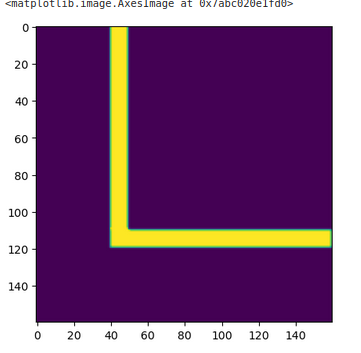
con eso ya se leen los archgivos, por ejemplo, podemos graficar
import matplotlib.pyplot as plt plt.imshow(data_array)
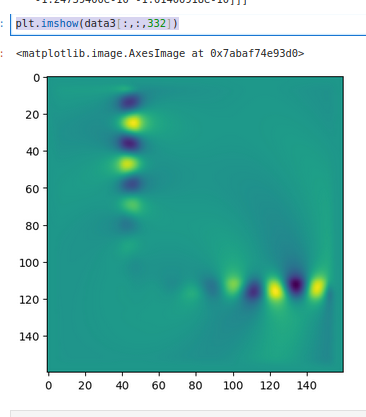
El campo electromagetico tambien lo podemos visualizar si hacemos
# Abre el archivo HDF5 en modo lectura
with h5py.File('ez.h5', 'r') as f:
# Muestra las claves principales del archivo
print(f"Claves principales del archivo: {list(f.keys())}")
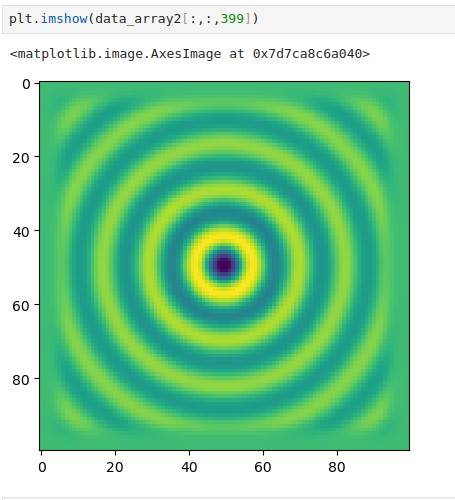
plt.imshow(data3[:,:,332])
# Abre el archivo HDF5 en modo lectura
with h5py.File('ez.h5', 'r') as f:
aux1 = f['ez']
# Convierte el dataset a un arreglo de numpy
aux2 = np.array(aux1)
plt.imshow(data3[:,:,332])
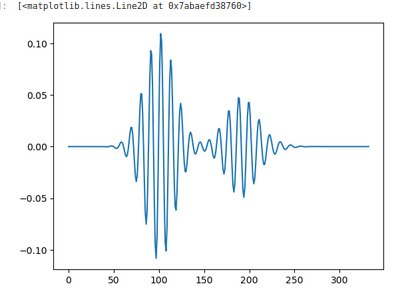
plt.plot(data3[40,40,:])
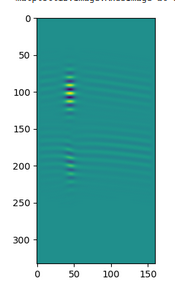
plt.imshow(data3[40,:,:].transpose())
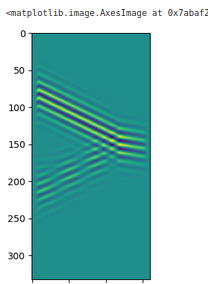
plt.imshow(data3[:,40,:].transpose())
h5topng -t 0:332 -R -Zc dkbluered -a yarg -A eps-000000.00.h5 ez.h5 convert ez.t*.png ez.gif

A 90 bend
Este es el manual, del manual…, vamos a analizar lo que viene en https://meep.readthedocs.io/en/master/Python_Tutorials/Basics/
# From the Meep tutorial: plotting permittivity and fields of a bent waveguide
import meep as mp
cell = mp.Vector3(16, 16, 0)
geometry = [
mp.Block(
mp.Vector3(12, 1, mp.inf),
center=mp.Vector3(-2.5, -3.5),
material=mp.Medium(epsilon=12),
),
mp.Block(
mp.Vector3(1, 12, mp.inf),
center=mp.Vector3(3.5, 2),
material=mp.Medium(epsilon=12),
),
]
pml_layers = [mp.PML(1.0)]
resolution = 10
sources = [
mp.Source(
mp.ContinuousSource(wavelength=2 * (11**0.5), width=20),
component=mp.Ez,
center=mp.Vector3(-7, -3.5),
size=mp.Vector3(0, 1),
)
]
sim = mp.Simulation(
cell_size=cell,
boundary_layers=pml_layers,
geometry=geometry,
sources=sources,
resolution=resolution,
)
sim.run(
mp.at_beginning(mp.output_epsilon),
mp.to_appended("ez", mp.at_every(0.6, mp.output_efield_z)),
until=200,
)
en este ejemplo modificamos la fuente
# From the Meep tutorial: plotting permittivity and fields of a bent waveguide
import meep as mp
cell = mp.Vector3(16, 16, 0)
geometry = [
mp.Block(
mp.Vector3(12, 1, mp.inf),
center=mp.Vector3(-2.5, -3.5),
material=mp.Medium(epsilon=12),
),
mp.Block(
mp.Vector3(1, 12, mp.inf),
center=mp.Vector3(3.5, 2),
material=mp.Medium(epsilon=12),
),
]
pml_layers = [mp.PML(1.0)]
resolution = 10
fcen = 0.15 # pulse center frequency
df = 0.1 # pulse width (in frequency)
sources = [mp.Source(mp.GaussianSource(fcen,fwidth=df),
component=mp.Ez,
center=mp.Vector3(-7, -3.5),
size=mp.Vector3(0, 1),
)
]
sim = mp.Simulation(
cell_size=cell,
boundary_layers=pml_layers,
geometry=geometry,
sources=sources,
resolution=resolution,
)
sim.run(
mp.at_beginning(mp.output_epsilon),
mp.to_appended("ez", mp.at_every(0.6, mp.output_efield_z)),
until=200,
)
se crearon archivos h5, esa fue el output, podemos checar cuales son los archivos con la instrcccion
ls *h5
la cual es valida para cuando esta en el notebook jupyter o cuando estas en el promt en linux, los archivos son dos h5, en el proximo post vamos a ver como se pueden leer en python
eps-000000.00.h5 ez.h5